Π
Patron naszej szkoły- Adam Adamandy Kochański jak każdy z was wie (albo przynajmniej powinien), był m.in. świetnym matematykiem. Z tej dziedziny, jego z największych dzieł jest na pewno koncepcja retyfikacji okręgu (mówiąc prościej wyprostowanie okręgu).
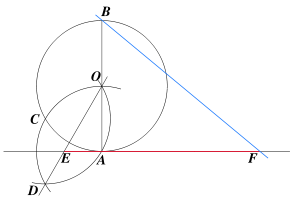
Obrazek, który widzicie powyżej, to konstrukcja liczby π Kochańskiego. Budowa jej przebiega mianowicie tak: rysujemy okręg i zaznaczamy na jego środku O między nim, a promieniem ,,a" prowadzi się średnicę AB. Następnie z punktu A zakreślamy łuk okręgu rozwartością cyrkla równą a, w przecięciu z okręgiem wyjściowym otrzymuje się punkt C; z tego punktu tą samą rozwartością a cyrkla zakreślamy kolejny łuk. Punkt D, który widzicie (w tej chwili mieliście patrzeć na rysunek!) jest punktem przecięcia obu zakreślonych łuków. Dalej w punkcie A kreśli się następnie styczną do okręgu OD odkłada się odcinek EW(nie to żeby to były moje inicjały) o długości 3a. Odległość BF jest równa w przybliżeniu długości połowy okręgu.
Myślę, że zbudowanie takiego układu to niezła zabawa. Warto jeszcze wspomnieć, iż Kochański pomylił się w tej konstrukcji ok. 0,01%. Jak dobrze wiecie to bardzo mały błąd.
Chciałabym jeszcze wspomnieć coś o liczbie π inaczej ludolfinie. Otóż jest to stała matematyczna określana jako stosunek długości okręgu koła do długości jego średnicy. Jest to liczba niewymierna i przestępna. π jest także 16 liczbą alfabetu greckiego.
Tak więc nasz patron był pierwszym konstruktorem tak dokładnego przybliżenia geometrycznego liczby π (tak a propos czyta się ,,pi").
Mamy więc być z czego dumni.
Myślę, że zbudowanie takiego układu to niezła zabawa. Warto jeszcze wspomnieć, iż Kochański pomylił się w tej konstrukcji ok. 0,01%. Jak dobrze wiecie to bardzo mały błąd.
Chciałabym jeszcze wspomnieć coś o liczbie π inaczej ludolfinie. Otóż jest to stała matematyczna określana jako stosunek długości okręgu koła do długości jego średnicy. Jest to liczba niewymierna i przestępna. π jest także 16 liczbą alfabetu greckiego.
Tak więc nasz patron był pierwszym konstruktorem tak dokładnego przybliżenia geometrycznego liczby π (tak a propos czyta się ,,pi").
Mamy więc być z czego dumni.